ILMU ALAMIAH DASAR : GRAF

TEORI GRAF

Kelahiran teori Graf

Sejarah Graf : masalah jembatan Konigsberg (1936)

Graf yang merepresentasikan jembatan konigsberg :

            Simpul (vertex) : menyatakan daratan

            Ruas (edge) : menyatakan jembatan

Definisi non-formal dari Graf dalam kamus webster (1913)

Graf mempunyai dua pengertian :

1.      Suatu kurva atau permukaan, letak (locus) dari suatu titik dimana kordinat-kordinatnya merupakan variabel-variabel dalam persamaan letak

2.      Suatu diagram yang melambangkan suatu sistem keterhubungan berdasarkan titik (spot), semua dapat saling dibedakan dan beberapa di hubungkan oleh garis sejenis

                                      

DASAR-DASAR GRAF

·         Suatu graf terdiri dari dua himpunan yang berhingga, yaitu himpunan titik-titik tak kosong ( simbol V(G) ) dan himpunan garis-garis ( simbol E(G) )

·         Setiap garis berhubungan dengan satu atau dua titik, titik tersebut di sebut titik ujung.

·         Garis yang berhubungan dengan satu titik disebut LOOP

·         Dua garis yang menghubungkan titik yang sama disebut GARIS PARALEL

·         Dua titik dikatakan berhubungan bila ada garis yang menghubungkan keduanya

·         Titik yang tidak punya garis yang berhubungan dengannya disebut TITIK TERASING

·         Graf kosong adalah graf yang tidak punya titik dan garis

·         Graf berarah adalah graf yang di semua garisnya memiliki arah

·         Graf tak berarah adalah graf yang semua garisnya tidak memiliki darah

DERAJAT GRAF

Derajat simpul V, ditulis d(v) adalah banyaknya ruas yang menghubungi v. Karena setiap ruas dihitung dua kali ketika menentukan derajat suatu graf, maka :

Jumlah derajat semua simpul suatu graf (derajat) = dua kali banyaknya ruas graf (size graf).

Suatu simpul disebut genap/ganjil tergantung apakah derajat simpul tersebut genap/ganjil. Kalau terdapat self-loop, maka self-loop dihitung 2 kali pada derajat simpul.

Vertices : Mode : Objek

Edge : Sisi : Garis

G (V, e)

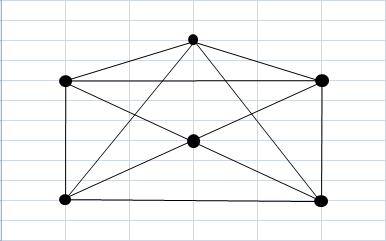
CONTOH GRAF DERAJAT 3

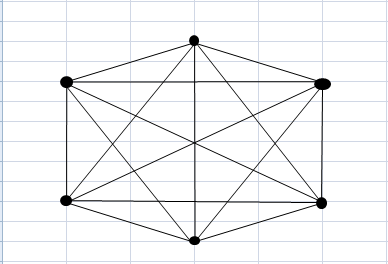
CONTOH GRAF DERAJAT 4

CONTOH GRAF DERAJAT 5

VIDEO CARA MEMBUAT GRAF DERAJAT 3

VIDEO CARA MEMBUAT GRAF DERAJAT 4

VIDEO CARA MEMBUAT GRAF DERAJAT 5

referensi :
sainsmat.uksw.edu/2008/wp-content/uploads/2010/03/mastergraf.pdf
http://rifki_kosasih.staff.gunadarma.ac.id/Downloads/files/37568/Bab+1+-+Dasar+Teori+Graf.pdf
http://yohananugraheni.files.wordpress.com/2010/11/teori-graf-complete.ppt